1-10 ウェブレットの種類
特に実用的であることが証明されている何種類かのウェブレットがこのツールボックスに含まれています。
ここでは、これらのウェブレットについて説明します。”Wavelet Display”ツールを引き出せば、
ウェブレットについて詳しく調べることができる。
①MATLABコマンドラインからwavemenuを入力します。すると、Wavelet Toolboxのメインメニューが表示されます。
②”Wavelet Display”というメニューアイテムをクリックします。すると、”Wavelet Display Tool”が表示されます。
③ツールの右上のメニューでのウェブレットメニューから種類を選びます。
④Displayボタンをクリックします。ウェブレットの図とそれに関連するフィルタが現れます。
⑤右に位置する”Information Bottons”をクリックすることで、さらに多くの情報が得られます。
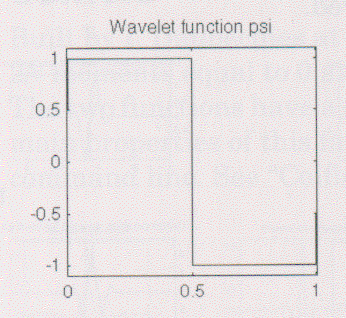
Haar
ウェブレットに関するどんな議論でも最初は最も単純なHaarから始まります。
Haarは離散的で、step関数に似ています。これは、Daubechies db1と同じウェブレットを表す。
詳細については、p64のHaarを見よ。
Daubechies
ウェブレット研究の世界で輝かしい功績を挙げた人の一人であるIngrid Daubechiesさんは、
離散ウェブレット解析を実用的なものにする、
簡潔に支援された正規直行ウェブレットと呼ばれるものを発明した。
Daubichies Family Waveletの名前は、dbNで表記され〈ここで、Nは次数、dbはウェブレットのあだ名である。
〉
上で述べたように、ウェブレットdb1はHaarと同じである。ウェブレットの次に9個を以下に示す。
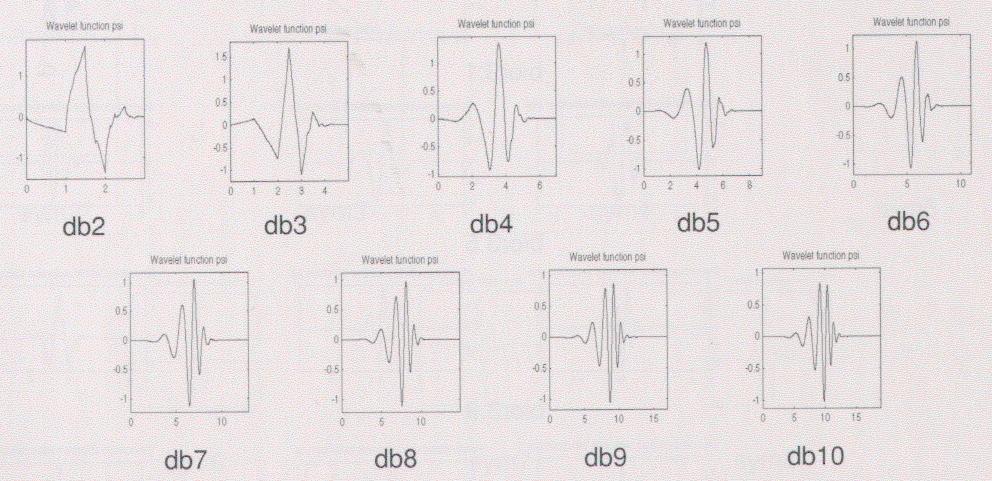
MATLABで「waveinfo('db')」と入力することでこの種のウェブレットの主な性質の要点を得ることができます。
「Daubechies」の詳細については、p6-63「Daubichies Wavelets;dbN」を参照しましょう。
Biorthogonal
この種のウェブレットは、信号と画像に復元を必要とされる、線形位相の性質を示します。
復元のためのものと、同じものの代わりに分解のためのもう一つの2つのウェブレットを
利用することによって、面白い性質が導かれる。
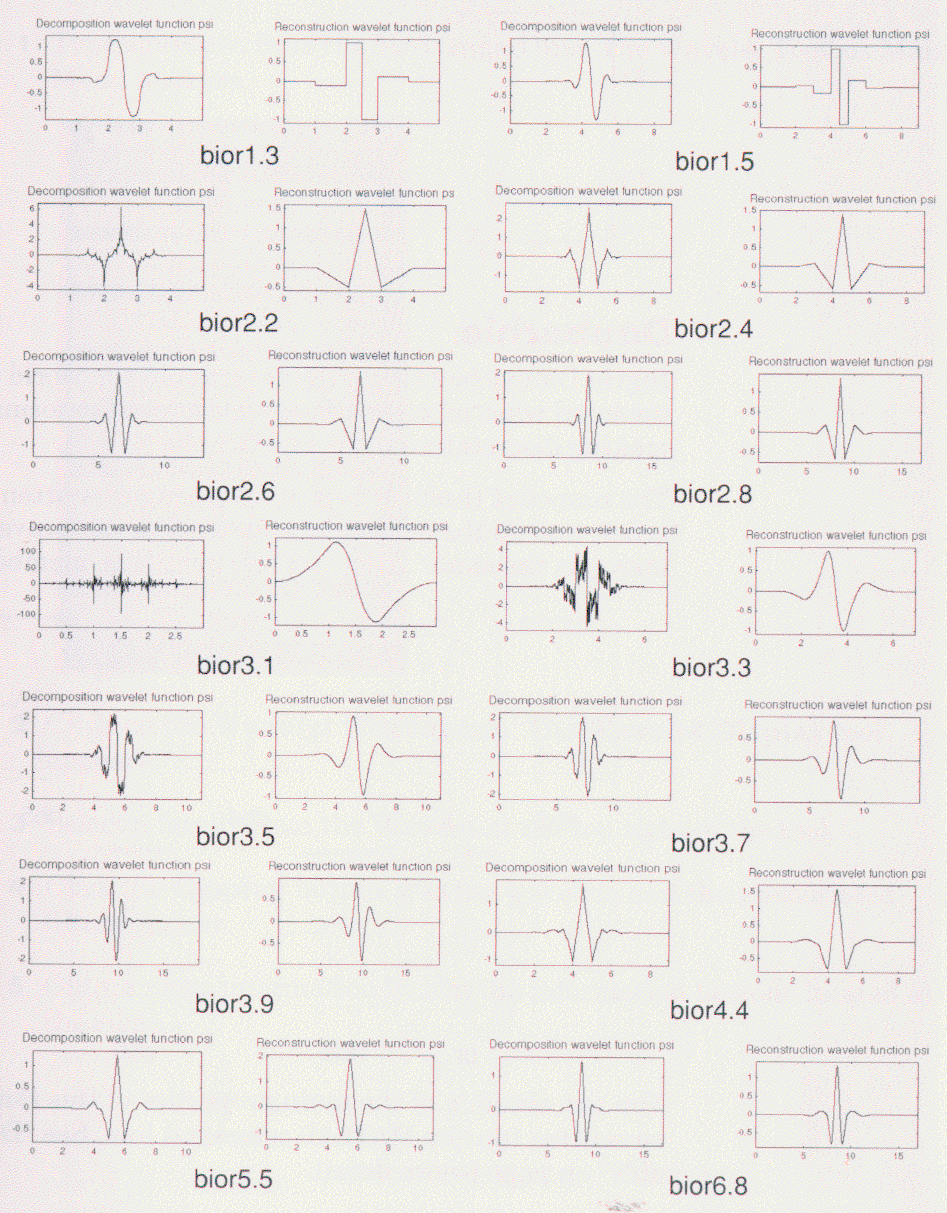
MATLABのコマンドラインから「waveinfo('bior')」を入力することでこの種のウェブレットの主な
特性の要点を得ることができます。詳細については、p6-67の「Biorthogonal Wavelet Pairs: biorNr.Nd」
を参照しましょう。
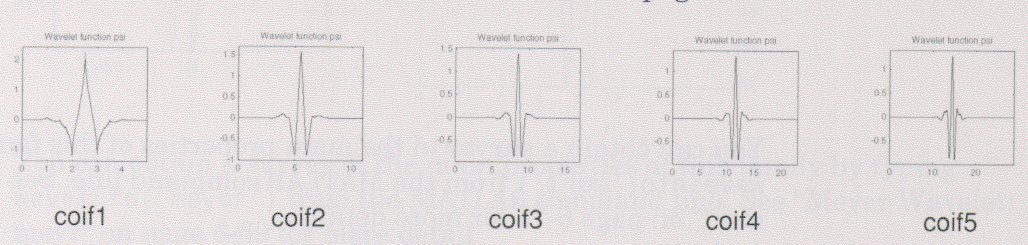
Coiflets
R.Coimanの要請でI.Daubechiesによって作られた、このウェブレット関数は
0に等しい2Nモーメントをもち、そのスケーリング関数は0に等しい2N-1モーメントをもつ。
この2つの関数は長さ6N-1のサポーターをもつ。
MATLABのコマンドラインから「waveinfo('coif')」を入力することによって
することでこの種のウェブレットの主な特性の要点を得ることができます。
「Coiflets」の詳細については、p6-66の「Coiflet Wavelets: coifN」を参照しましょう。
Symlets
Symletsはdbウェブレットを修正したもので、Daubechiesは提案したほぼ対称的なウェブレットであります。
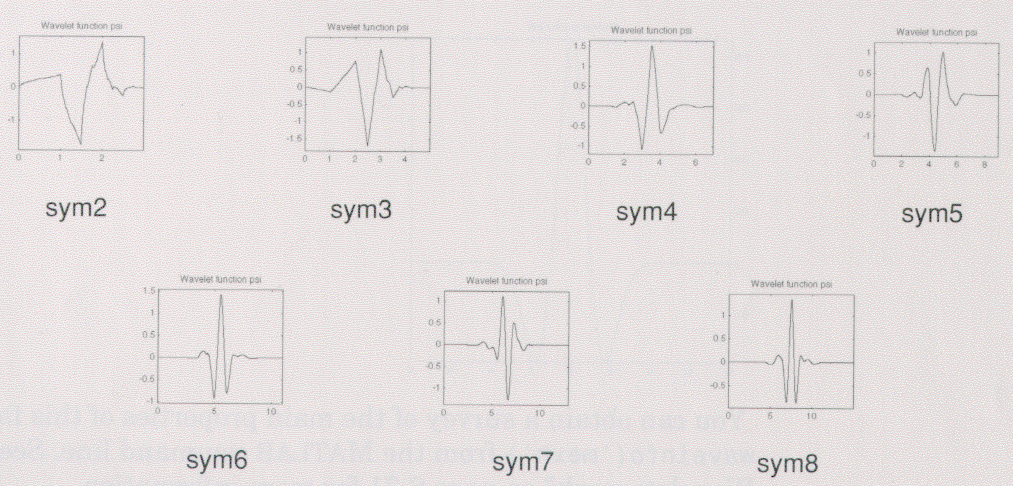
MATLABのコマンドラインから「waveinfo('sym')」を入力することでこの種のウェブレットの主な
特性の要点を得ることができます。詳細については、p6-65の「Symlet Wavelets: symN」
を参照しましょう。
font size="+2">Morlet
このウェブレットはスケーリング関数を持っていない。しかし、明瞭である。
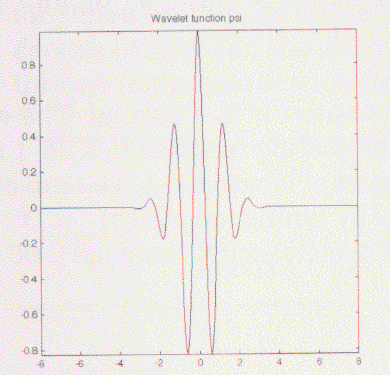
MATLABのコマンドラインから「waveinfo('morl')」を入力することでこの種のウェブレットの主な
特性の要点を得ることができます。詳細については、p6-72の「Morlet Wavelet: morl」
を参照しましょう。
font size="+2">Mexican Hat
これもスケーリング関数を持っていなく、ガウス確率密度関数の2次導関数に比例する関数から導かれている。
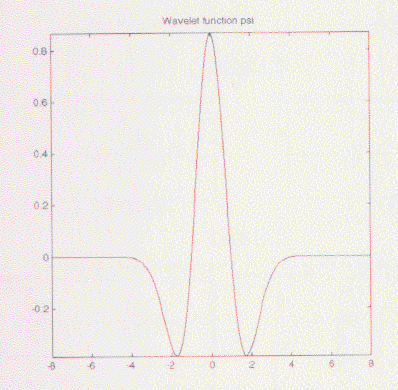
MATLABのコマンドラインから「waveinfo('mexh')」を入力することでこの種のウェブレットの主な
特性の要点を得ることができます。詳細については、p6-71の「Morlet Wavelet: morl」
を参照しましょう。
font size="+2">Meyer
Meyer Waveletとスケーリング関数は周波数領域で定義されている。
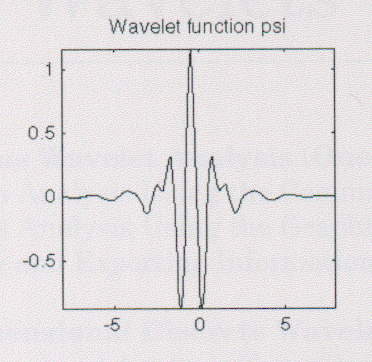
MATLABのコマンドラインから「waveinfo('meyer')」を入力することでこの種のウェブレットの主な
特性の要点を得ることができます。詳細については、p6-69の「Meyer Wavelet: meyer」
を参照しましょう。
【
BACK
】 【
NEXT
】








