フーリエ解析の基礎である正弦波と、ウェブレットを比べてみよう｡ 正弦波の継続時間は有限でなく、マイナス無限大からプラス無限大までおよぶ。
正弦波は滑らかで先が予想できるが、
ウェブレットは不規則で非対称な傾向がある。

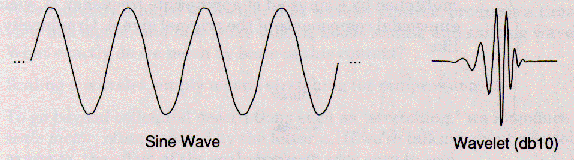
フーリエ解析は、信号を様々な周波数の正弦波に分解する。 同様に、ウェブレット解析は、様々に拡大・縮小・移動された オリジナル(マザー)ウェブレットに、信号を分解する｡

ウェブレットと正弦波の図を見比べただけでも、 滑らかな正弦波より不規則なウェブレットのほうが、 鋭い変化をする信号を解析するのに適していると、直感的にわかるだろう。

これは、局所的な範囲を持つウェブレットによって、信号の局所的な特徴がよりよく表現できることを意味する｡

次元数

ここまでは、普通の信号を取り巻く１次元のデータだけについて議論してきたが、
ウェブレット解析は画像のような2次元のデータや、原理的には、より高い次元のデータにも適応できる。

MATLABのツールボックスは１,２次元解析技術だけを扱う｡