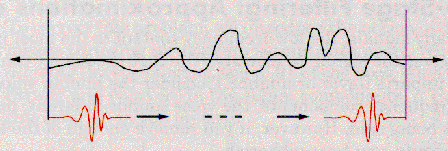
数学的には、フーリエ解析の過程は、
フーリエ変換:
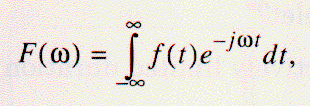
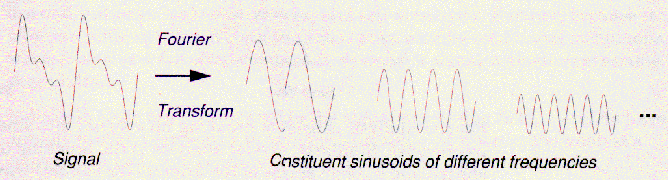
によってあらわされる。 上式は、複素指数関数によって増幅された信号f(t)の足し合わせである。
(複素指数関数は、実数・虚数の正弦波成分に分解できることを思い出そう。)
その変換の結果はフーリエ係数F(ω)であり、このフーリエ係数F(ω)は適切な周波数ωの正弦波を増幅したときに、
オリジナル信号の正弦波成分を生み出す。この過程は、下図のようなものである。
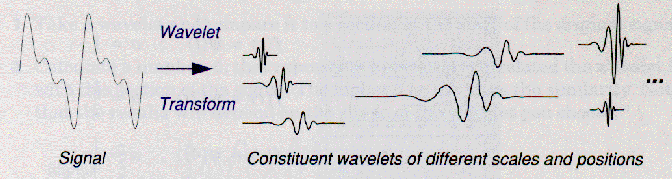
同様に、連続ウェブレット変換(CWT:Continuous Wavelet Transform)は、下式のように定義される。
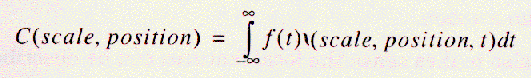
これは、拡大・縮小、移動されたウェブレット関数Ψによって増幅された、信号の足し合わせとして定義される。
連続ウェブレット変換の結果は、たくさんのウェブレット係数Cであり、
Cはscaleとpositionの関数である。
適切に拡大・縮小、移動されたウェブレットを増幅することは、オリジナル信号のウェブレット要素を生み出す。
スケーリング
すでに、ウェブレット変換が 信号の時間-スケール視点を提供することは述べたが、 ここでは、ウェブレットのスケーリングとシフティングについて説明する。
スケーリングとは、簡単に言うと、 ウェブレットを伸ばしたり縮めたりすることである。
スケーリングには、スケールファクター"a"を用いる。
正弦波を例にすると、スケールファクターの効果が簡単に見てとれる:
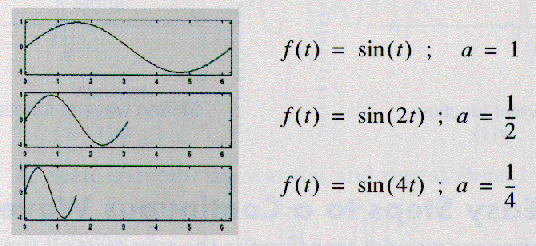
スケールファクターの働きは、ウェブレットでも同様である。
より小さなスケールファクターは、より圧縮されたウェブレットを意味する。
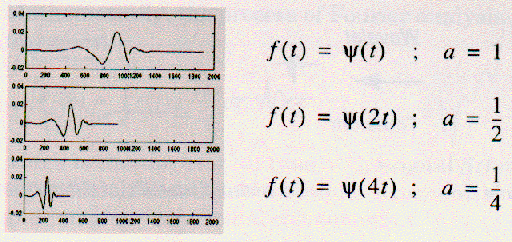
上の図からも明らかなように、正弦波 sin(ωt)において、
スケールファクターaは角周波数ωの逆数の関係にある。
同様に、ウェブレット解析においても、スケールは信号の周波数に関係する。
このことについては、あとで詳しく説明する。
シフティング(移動)
シフティングとは、簡単に言うと、
ウェブレットの始まりを遅らせたり、早めたりすることである。
数学的に、関数f(t)をkだけ遅らせることは、f(t-k)によって表される。
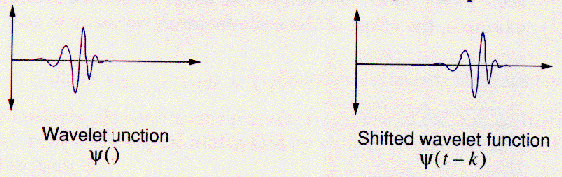
連続ウェブレット変換の五つの行程
連続ウェブレット変換は、拡大・縮小、移動されたウェブレットによって
増幅されたすべての信号の足し合わせである。
この行程はウェブレット係数を作り出し、そのウェブレット係数はscaleとpositionの関数である。
それは非常に簡単な行程であり、実際、連続ウェブレット変換を行うための簡単な五つの行程を以下に示す。
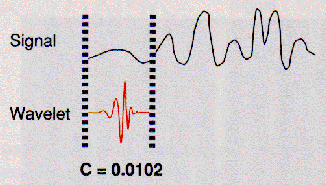
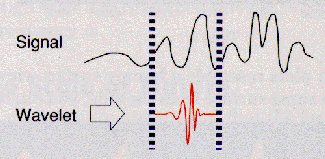
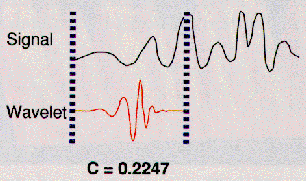
|
これらのすべての係数がどのように意味をなすか?
x軸は時間、y軸はスケール、x−y点のそれぞれの色は
ウェブレット係数Cの大きさを表す図を、作ることができるであろう。
これはグラフィカルツールで作られた、係数図である。
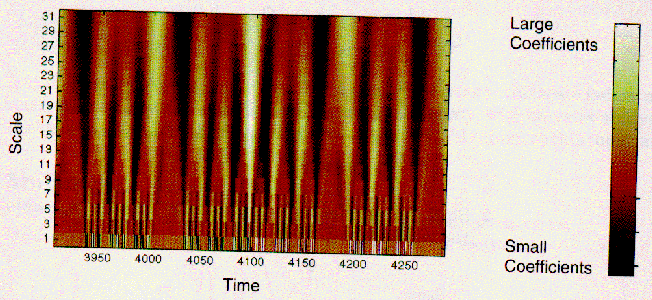
この係数図は、でこぼこな面を真上から見たものに似ている。
もしこれを横から見たら、下図のように見えるだろう。
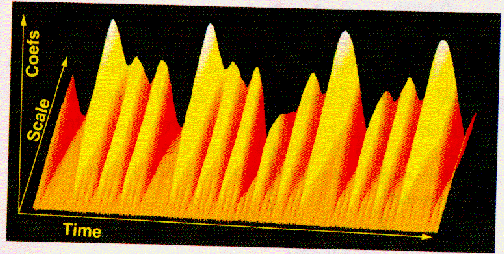
連続ウェブレット変換の係数図は、まさに前のほうで述べた信号の時間-スケール視点である。 これは、時間-周波数のフーリエ視点とは異なる信号データの見方だが、 これらは無関係ではない。
スケールと周波数
上図の係数図において、y軸のスケールの目盛りが
1から31まであることに注目しよう。
より大きいスケールが、より波長の長いウェブレットに
対応することは前にも述べた。
ウェブレットの中でより波長の長いものは、比較される信号の部分の中でより長いものに対応する。
したがって、ウェブレット係数によって、信号の特徴の粗さが測定されることになる。

したがって、ウェブレット解析によって表された、 ウェブレットのスケールと周波数の間には次のような関係がある:
・小さいスケール a ⇒ 短い波長のウェブレット ⇒急に変化する細部 ⇒ 高周波数ω
・大きいスケール a ⇒ 長い波長のウェブレット ⇒ ゆっくり変化する大まかな特徴 ⇒ 低周波数ω
自然のスケール
ウェブレット解析が時間-周波数視点を作り出さないことは、 技術的な弱点ではなく、強みであることを理解することは重要である。
時間-スケール視点は、データの見る異なった方法であるだけではなく、 数多くの自然現象から得られたデータを見るとても自然な方法である。
下図のような、巨大なものから塵のようなものまで様々な大きさの隕石が長年にわたり
衝突した結果である月のでこぼこな表面を、考えてみよう。
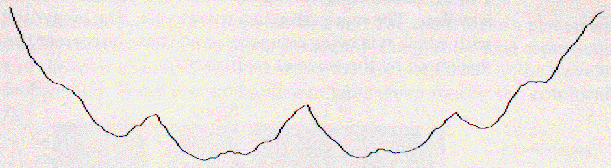
この表面の断面を一次元信号として考えると、
これは様々なスケールの要素を持った信号として扱うことが出来る。
大きな特徴は巨大な隕石よってつくられたもので、
微細な特徴は小さな隕石によってできたものである。
このような場合では、周波数で考えるよりスケールで考えたほうが意味をなす。
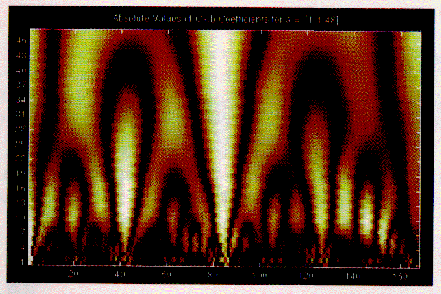
この信号は人工的につくられたものだが、 血管や樹の分岐や、山や砕かれた金属のぎざぎざの表面などの 多くの自然現象にとって、スケールによる解析は役立つものである。
連続ウェブレット変換の"連続"とはどういううことか?
現実世界のデータを使っていも、コンピュータで処理するには、 離散信号(離散的時間間隔で測定された信号)として扱わなければならない。 つまり、連続ウェブレット変換も、離散的時間で行われている。 それでは、連続ウェブレット変換の"連続"とは、正確にはどういうことなのか?
連続ウェブレット変換の"連続"は何を意味するだろうか?また、何をもって離散ウェブレット変換と区別するだろうか? 連続と離散ウェブレット変換の違いは、スケールにある。 (離散ウェブレット変換については後で述べる。)
離散ウェブレット変換とは異なって、連続ウェブレット変換は、オリジナルの信号のスケールを上限として
オリジナルの信号のスケールをから自分で決めた最大のスケールまで、すべてのスケールについて実行することができる。
(そのとき、スケールは求める解析精度と利用できるコンピュータの計算能力を考えながら決めることになる。)
連続ウェブレット変換は移動についてもやはり連続的である。すなわち、計算している間、 解析しているウェブレットは、解析対象の関数の全範囲にわたって、徐々に移動される。