|
MIRS2009 OpenCV�ɂ�鐔���F�� |
|
MIRS0901-SOFT-0010 |
|
�@�Ő� |
�ŏI�X�V�� |
�쐬 |
���F |
�����L�� |
|
A01 |
2009/11/15 |
��� |
���� |
���� |
|
A02 |
2009/11/21 |
��� |
���� |
DB�̎d�l�ɍ��킹�ăv���O�����̉���&�o�O�E�s��C���@�Y�t�\�[�X�̓Y�t |
|
A03 |
2009/12/26 |
��� |
���� |
�d�l�ύX 2�l���A���S���Y���̕ύX�@�o�O&�s��C�� �Y�t�\�[�X�̍X�V |
|
A04 |
2010/01/12 |
��� |
���� |
�o�O&�s��C�� �Y�t�\�[�X�̍X�V |
|
A05 |
2010/02/06 |
��� |
���� |
�Y�t�摜�E�d�l�����Z��{�Ԃ̂��̂ɕύX�A�Y�t�\�[�X�̍ŏI�X�V |
1.�ړI
2.�d�l
3.�T�v
4.���쎎��
5.�܂Ƃ�
1 �ړI
�{�h�L�������g��OpenCV��p���������F���A���S���Y���ɂ��Ă܂Ƃ߂����̂ł���B
2 �d�l
�@�O������F ���̐����F���v���O�����͈ȉ��̑O������̉��ɍ쐬�����B
�E2�̐�����������Ă���DB���قڐ��ʂ���J�����ő����Ă���
�EDB�{�[�h�� �w�i�����F�A�����������F�ŕ`����Ă���Ƃ���
�EDB�{�[�h�ɕ`����Ă��鐔����7�Z�O�����gLED�̂悤�Ȑ����ł���Ƃ���
�@�B���ڕW�F �Œ�ł��ȉ��̎��������͒B���ł���悤�ɂ���
�E0�`9�܂ł̂��ׂĂ̐����̔��ʂ��i�u2�v�Ɓu5�v�̋�ʂ��j�ł���悤�ɂ���
�E2�̒l���Ɂi���̃L���v�`���s���Łj���f�ł���悤�ɂ���
�E2�̒l�̑��Έʒu(�ǂ��炪�E�łǂ��炪����)�f�ł���悤�ɂ���
�E�����̌X����c�݂��l���ł���悤�ɂ���
�d�l(���Z��I�����_)
�E
�J�����Ŕw�i�@���@������ ����DB��S�đ������
�������荞�݁A�O���[�X�P�[���ɂ��2�l���i+��Â̎�@�j���s���A���x�����O�A�g���~���O���s�������
�Ǝ��i�H�j�̃A���S���Y����p�������F�����s���B
�E�@�@2�̐������ɔF�����A���Έʒu(�E�ɂ��邩���ɂ��邩)�ʂ���
�E
�p�x��A�n�t�ϊ��Ȃǂ̃A���S���Y���͗p���Ă��Ȃ�
�E�@�@���Z��̎��Ԃ��͂����肵�āA�uDB�����̂�����Ƌ��Z��Ǎŏ㕔�ɂ��鍕���e�[�v���q�����āA�����������傫�ȍ��F�̗̈������Ă���v
�@���Ƃ��킩���Ă��܂����̂ŁA���x�����O��A�ʐς̈�ԑ傫�����̂����O���邱�ƂŐ��l���̒��o���s���Ă���B
�E�@�@���i�K�ŁA�ŏ��ŗL�l�@�ɂ��R�[�i�[���o���\(�����F���v���O�����ɂ͒��ڂ�������Ă��Ȃ�)
3 �T�v
�ȉ��ɁA�����F���̈�A�̗���̊T�v������
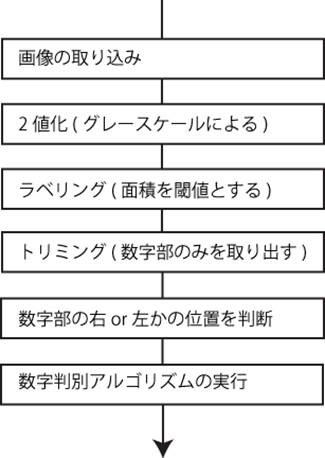
fig.1 �����F���t���[�`���[�g
�e�`���[�g�ɂ��ċL�q����
1. �摜�̎�荞��
uvccapture��p�����L���v�`�����s���AcvLoadImage����p���Ă��̉摜�����\���̂Ɏ�荞��
�@�@�@�W���v���O������img_update�������̂܂g�킹�Ă�������B
2.�@�O���[�X�P�[���ɂ��2�l��
�@�@�@�摜���A��߂�臒l�ɏ]���āA��(255)�ƍ�(0)�̓�̒l�ɕ��ނ���B
�@�@�@�W���v���O�����ł�HSV�\�F�n��p����2�l�����s���Ă��邪�A�����ł́u�Ώې������h���h�Ŕw�i���h���h�v�Ƃ����O������̉��ōs���Ă���̂ŁA
�@�@�O���[�X�P�[���i1�p�����[�^�ɂ�鍕(0)~��(255)�܂ł̒l��p����\�F�n�j�ɂ��2�l���ł��قƂ�ǎx�Ⴊ�Ȃ��ƍl���A�����p�����B
�@�@�@2�l���̃A���S���Y���ŁA�u��Â̎�@�v�Ȃ���̂�����A�����2�l����臒l���Œ肷��̂ł͂Ȃ��A�摜�̏ɍ��킹�Ď����ʼnς��Ă����Ƃ������̂ł���B
�@�@�ʏ�̌Œ�臒l�ɂ��2�l���ł́A�����ꏊ�œ����p�x�ŎB�e�����ɂ�������炸�A2�l�����ʂ��傫���ς���Ă��܂��A���̂����Ń��x�����O������ɍs��ꂸ�A��������
�@�@�����s����Ƃ��������Ƃ��������B�����ő�Â̎�@�������ꂽ�Ƃ���A���̎�@��p����A�p�x��ꏊ�������ł���Ȃ�A2�l���摜���ʂ͂قƂ�Ǖϓ����Ȃ��Ƃ������Ƃ��킩�����B
�@�@�@�ȉ��ɁA�ʏ��2�l���摜�ƁA��Â̎�@��p����2�l���摜�������B
 �@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@
fig2. (a)�ʏ��2�l���摜 �@�@(b)��Â̎�@��p����2�l���摜
3.���x�����O
2�l�������摜���琔���������o����B�A�����Ă��锒�̕������ЂƂ̃O���[�v�ƍl���A�܂��A�ʐς�臒l�ɂ��A����傫���ȉ��̃O���[�v�͏��O
�@����Ƃ������t�B���^�����O���s���Ă���B
�@fig.3�ɁA���x�����O�̊T�O��}�I�ɕ\�������̂������B
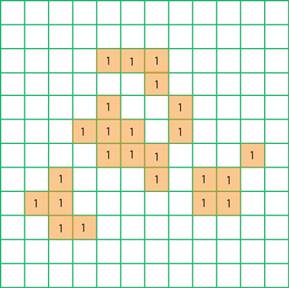 �@�@�@�@
�@�@�@�@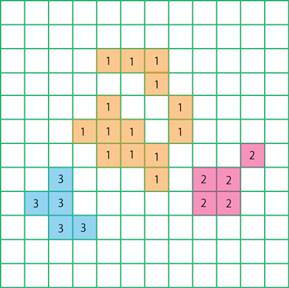
fig.3 (a)���x�����O�O�̑Ώۉ摜 (b)���x�����O��̑Ώۉ摜
fig4�ɁA���x�����O�̃A���S���Y���̃t���[�`���[�g�������B
�Ȃ��Afig.4�́@���X�^�X�L�����@�Ƃ́A�摜�̍��ォ��E���܂ő������s�����Ƃ������B
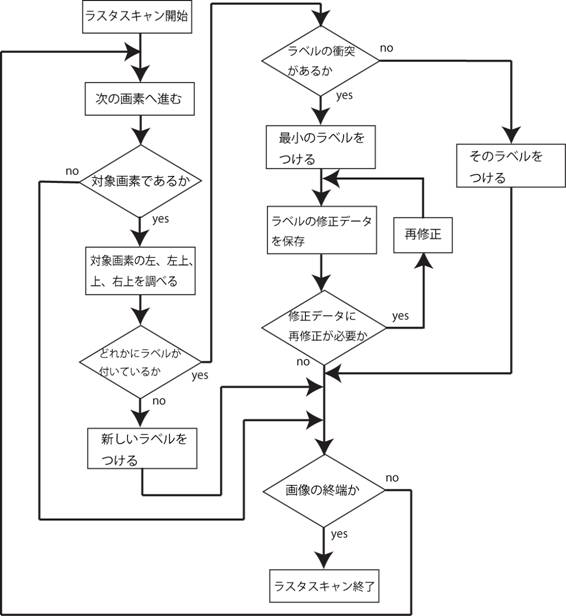
fig.4 ���x�����O�̃t���[�`���[�g
3.5. DB���������o
�@�����DB�̎d�l�������Ƃ��됔�����Ɛ������̊ԂɁA��{�̒��������������邽�߁A����𗘗p���ADB�̒��S�����m���A�摜�F�����s���̕����̂��߂̏��ɉ����悤�ƍl�������̂ł���B
�������A����͋��Z��J�n���O�Ɏv�����ō�������̂ł���A�����Ɍ����Ɓ@�M�����͍����Ȃ�
�@�������A�����Ă��}�C�i�X�ɂ͂Ȃ�Ȃ��Ǝv���A���݂���M�����̂܂܂ł���B�@�����͂��������M�����̍����Ȏd�l�ɂ��悤�Ƃ͎v���Ă���B
4. �g���~���O
���x�����O�����摜����A������(���̕���)��S�ē����ŏ��̋�`�̈���v�Z���A�摜������B
�@�ȉ��̐}�̂悤�ɁA4�̃p�^�[���ő������A���߂����̈�̎n�_�E�I�_�̍��W��������B
�}�̂悤�ɑ������A�͂��߂ďo�������(��)���e�_��x���W�Ay���W�ɐݒ肷��B4�̑�����2�_��x,y���W��������B
�@
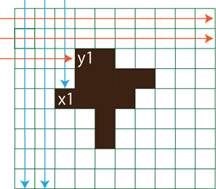
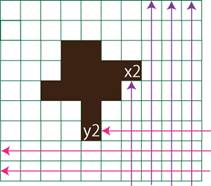
fig.5 �g���~���O�̃A���S���Y��
(a)�n�_ �@�@�ib�j�I�_
5. �����̈ʒu���f
�@�@����̋��Z��ł́AT���H�ɐ������Q����ł��āA�E�̐����ɂ͉E�����ɂ���d�|���A���̐����ɂ͍������ɂ���d�|����������Ă���̂ŁA
�@���������̔��ʂ����邾���ł͂Ȃ��A���̂Q�̐����̑��Έʒu��m��Ȃ���Ȃ�Ȃ��B
�@�@2�̉摜�ɂ����āA4�̃g���~���O�ŋ��܂����n�_�i�������͏I�_�j��x���W�̔�r�����邱�Ƃ�2�̉摜�����E�̂ǂ���Ɉʒu���Ă��邩��m�邱�Ƃ��ł���B
6. �������ʃA���S���Y��
�@�@����l�����A���S���Y���́A���Z��ŗp����ł��낤DB�̐�����7�Z�O�����g�����ł��邱�Ƃ܂��A�l�Ă������̂ł���B
�@�@������7�Z�O�����g�����ƌ��肵�Ă��邽�߁A�ėp���͏��Ȃ����A���̐����Ɋւ��Ă����͍����M�����������Ă���Ǝ������Ă���B
�@�@�@�ȉ��ɁA���̃A���S���Y���������B
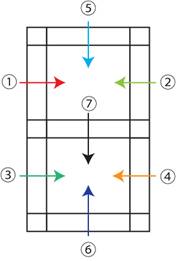
�T,fig5�̂悤�ɁA�g���~���O�����摜���A�V�̃p�^�[���ɂ�葖������B
���̍ہA�����͉摜�̒[�܂ōs�킸�A������x�ifig6�̂悤�ɐ������̈�ӂ��z�����炢�܂Łj�ŏI�����̂Ƃ���B
�U,�e�p�^�[���ɂ����āA��������(2�l���摜�ɂ�����u���v�����m)���������Ȃ��������̃f�[�^���i�[���Ă����B
�V,2�œ���ꂽ�f�[�^�����ƂɁA���̃f�[�^�̃p�^�[���ƈ�v���鐔����T���A���肷��B
�ȉ��̐}�́A0�`9�܂ł̐����ɂ�����p�^�[����}�I�Ɏ��������̂ł���B
fig6. ��������A���S���Y��
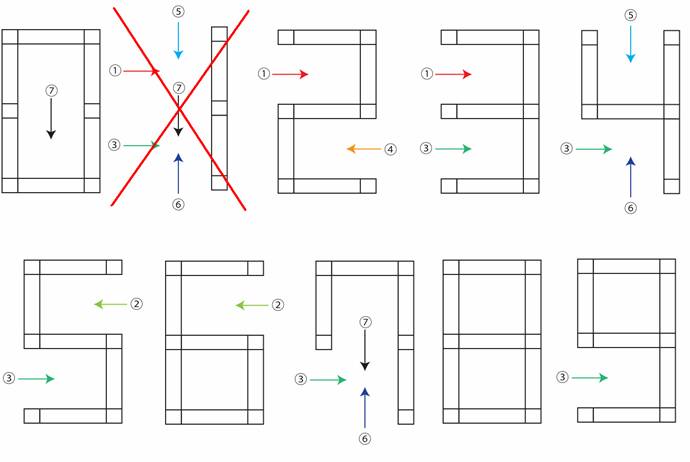
fig7.
�e�����ɂ�����A���S���Y���̓K�p
�@�E��L�̃A���S���Y���ł���ƁA�����́u1�v�̔��ʂ�����Ƃ��ɖ�肪�N����B
�@�@�@�@�@�@�@�u1�v���g���~���O����ƁA�����̋����������Ă��܂��̂ŁA��L�A���S���Y����p����Ɓu8�v�ƌ�F���Ă��܂��B
�@�@����ɑ��Ẳ�����E�ŊJ���
��L�A���S���Y�����s������A�g���~���O�摜�̏c������v�Z���A���ꂪ���ȏ�̒l�Ȃ�1�ƔF������B �Ƃ����d�l�ɂ����B
���_
7�̑��������邾���ŁA0�`9�܂ł̐�����S�Ẵp�^�[���ɕ��ނ��邱�Ƃ��ł���B
�W���v���O�����ł͕s�\�������u2�v�Ɓu5�v�̔��ʂ��\�ɂȂ����B
�����_������̂ł͂Ȃ��A�����т�����̂ŁA�M�����������B
�����̘c�݁i�߂�������X���Ă�����j�Ȃǂ͖����ł���B
���G�ȉ��Z��p���Ă��Ȃ��̂ŁA��������r�I����
���Z���s���O�ɁA�̈���i���ăT�C�Y�����������A����ɃA���S���Y���ł͉�f�P�ʂŃA�N�Z�X���Ă���̂ŁA��������r�I����
���_
����p����悤�Ȑ����݂̂ɂ����K���ł��Ȃ��̂ŁA�ėp�����Ⴂ
���̃A���S���Y����p����O�̃��x�����O�����܂������Ă��Ȃ��Ƃقڎ��s����
4 ���쎎��
�@����쐬�����v���O����������ȓ���Ɛ��������ʂ������邩������
�������i�{���Z��j
PC
:
OS:CentOS
5.4
MG3��CPU
�J���� :
Logicool�@Qcam E3500 (�W���@�Ɠ��l)
�Ώە��̂Ƃ̋��� ��50�`60cm
�s���g�͂����悻�Œ���
�ΏۂƂ��鐔���́A�u4�v�Ɓu2�v�ł���B
���s����
1.�摜�̎�荞��
 �@�@�摜�L���v�`����320�~240�̉𑜓x�ōs���Ă���
�@�@�摜�L���v�`����320�~240�̉𑜓x�ōs���Ă���
fig.8 �L���v�`���摜
2,�O���[�X�P�[���ɂ��2�l��
 �@�@�@�@�@
�@�@�@�@�@
fig.9 �@2�l���摜
�O���[�X�P�[�������s���A��Â̎�@��p����2�l�����s�����B
3, �ʐς�臒l�Ƃ������x�����O
 �@�@�@�@�@
�@�@�@�@�@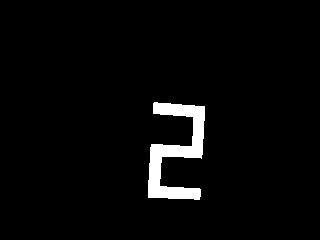
fig.10 (a)���x�����O�摜1 (b)���x�����O�摜2
�v���O�������ŁA���x�����O���ʂ���A�ʐς�2�Ԗڂɑ傫�����̂ƁA3�Ԗڂɑ傫�����̂𒊏o���Ă���B
4,�g���~���O
 �@�@�@�@�@�@
�@�@�@�@�@�@
fig.11
(a)�g�����摜1 (b)�g�����摜2
fig.11�̂悤�ɁAfig.9(a),(b)�̐�������������ŏ��摜������ꂽ�B
5. �����̈ʒu���f
�e��������x���W���擾����B(�g���~���O�̎��_�Ŋ��Ɋi�[����Ă���)
�@�@2�̉摜��x���W�̔�r�����A�E�ɂ���摜�Ȃ̂����ɂ���摜�Ȃ̂��f����B
6. �������ʃA���S���Y���̎��s
���Z���ł�terminal�ւ̏o�͕����͌���Ȃ��������A���_�Ƃ��ăS�[���ł����̂ŁA���������ʂ��Ă��ꂽ���Ƃ�������B
�ȏ�ɂ��A���̐����F���v���O�����͐���ɓ��삵�A�������l���邱�Ƃ����������B
5 �܂Ƃ�
�摜�����͌��݂�MG3��CPU�X�y�b�N�ł����Ȃ蕉�S�̑傫�������ł���B���̂��߁A�v���O�����̍������ƃ��\�[�X�̐ߖ�͕K�v�s���Ȃ��Ƃł���B
�@OpenCV�W���̃L���v�`������p����ƁA�����m���ŏ��������E�����~�X�����Ă��܂��悤�ł���B���i�K�ł�uvccapture�R�}���h��system���ŌĂяo���̂�����ł���B
�܂��AOpenCV�ł̃v���O���~���O�ł̓������̊m�ۂ������炩�Ȃ炸�J�����Ȃ��Ƃ�낵���Ȃ��B���������[�N���N�����Ă��܂����肷��ƍň�PC�������Ă��܂���������Ȃ��B
�@�摜�����v���O���~���O�̍������̋�̓I��@�Ƃ��Ă�
�]���ȗ̈�͂��炩���ߐ����āA�{���Ɍ�����������������������
double�^�͂Ȃ�ׂ��g�킸�Afloat�^�ŕ\�������݂�B(����́Adouble�^�������Đ錾����悤�ȍׂ��������͕K�v�Ȃ�����)�@�}�N���Œ�`���ꂽPI�Ȃǂ��������Ă݂�Ƃ�����������Ȃ��B
�\�ł���Ȃ�r�b�g���Z��p����(���݂̃R���p�C���͗D�G�Ȃ̂ł��܂�Ӗ��͂Ȃ���������Ȃ���)
����inline�W�J��p����B���Ƃ���inline�W�J��C++���L�̂��̂ł��������AC99�ł�inline�W�J���T�|�[�g���Ă���B
cvGet2D
cvSet2D �Ȃlj摜�ɃA�N�Z�X������͏������x���̂ŁA�Ώۉ摜�̉�f���i�[����Ă��郁�����̈�ɒ��ڃA�N�Z�X�����ق����f�R�����炵��(MIRS0902�}�l�[�W���[�������Ă���)
������̒�Ă�������Ď������܂����Ƃ��B
�������ǂ�����łɍs���Ɛ��x���ɒ[�ɗ����邱�ƂɂȂ邩������Ȃ��B�ǂ���s���ɂ��Ă��\���Ȓ��ӂ��K�v�ł���B
�v���O�����̃\�[�X�R�[�h���Q�l�܂łɍڂ��Ă���
linux��ō쐬�����t�@�C����windows�ŃA�[�J�C�u�����������Ȃ̂ŁA�u�������v�ŊJ���Ɖ��s�R�[�h�����킸�ɁA���Ɍ��Â炭�Ȃ�Ǝv����B
���̑������̃e�L�X�g�G�f�B�^�͉��s�R�[�h�̎������ʂ����Ă����͂��Ȃ̂ŁA�������Â炢�悤�Ȃ炻�̑��̃e�L�X�g�G�f�B�^�łǂ����B
linux�ł݂�ΊԈႢ�Ȃ��͂��ł��E�E�E
linux�̃^�[�~�i���ʼn𓀂������ꍇ��unzip�R�}���h�ł��g���Ă���������.�B
|
�֘A���� |