目次

1. maxon DC モーターの構造
2. モータの原理
3. DCモータとは
4. DCモータの概要
5. モータ特性カーブ
6. 駆動系のモータ仕様

maxon DC モーターの構造




モータの原理


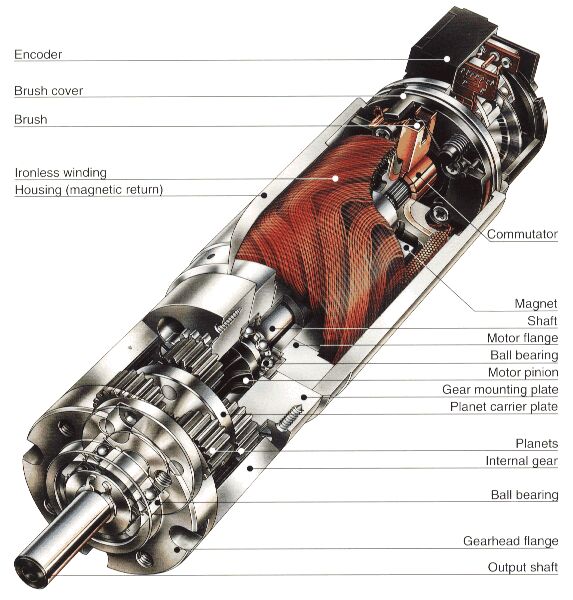
　MIRSに使われるモーターはDCモーターと呼ばれるものでその構造はモーター内に固定された永久磁石(マグネット)と、 鉄心にコイルを巻いたアマチュア(ローターとか電機子と呼ばれる)からなる。
　このアマチュアは2,3くらいにわかれ、このわかれた１つ１つを極と呼び、極が2つのものは2極モーター、3つのものは3極モーターと呼ぶ。 そしてこの極にコイルが巻かれている。 アマチュアのコイルには整流子(コミュテータ+ブラシ)と呼ばれる機械的接点を介して電流が供給される。 永久磁石により作られた磁界の中にコイルが置かれており、この磁界の強さとコイルを流れる電流の強さ、コイルの巻き数がモータの発生する取るに比例する。 電流を流すことによりある極が磁石になりローターの回転が始まる。 そして回転によってブラシの位置が変わり、次のコイルに電流が流れる。 これを繰り返すことにより、モーターは回転を続けるのである。 電気的には下記に示すようにフレミングの左手の法則でまずトルクが発生する。 モーターが回り始めると今度は磁界の中をコイルが動くことになる。 これによりこのコイルにはフレミングの右手の法則によって電圧が発生する。 この電圧のことを逆起電力といい、この伝あるを外部から加える電圧から引いた電圧に対応してコイルに電流が流れることになる。 この差し引いた電流によってモーターに発生するトルクが決まる。 したがってこの逆起電力が大きいとモータの最高回転数は低くなる。 これらを数式で表すと次のようになる。


a.)モーターに発生する力Fはフレミングの左手の法則より
F(t)=2πrNBi(t)=K_Ti(t)
where:
N：コイルの巻き数
r：コイルの半径
i(t)：電流
B：磁速密度
K_T=2πrNB：トルク定数、推力定数

b.)電気系の方程式はキルヒホッフの法則により次式が成り立つ。
Ld(i)/dt+Ri(t)=E(t)-e_i(t)
where:
L,R：コイルのインダクタンスと抵抗
E(t)：コイルへの印加電圧
e_i(t)：逆起電力


また、フレミングの右手の法則より
e_i(t)=2πrNBv(t)=K_ev(t)
where:
v(t)：コイルの移動速度
K_e=2πrNB：逆起電力定数

　上のことより次のことが考えられる。
トルクはFに比例するのでフレミングの左手の法則より、i(t)に比例することが分かる。 また回転数Nはコイルの移動速度v(t)がに比例する。 そしてフレミングの右手の法則より逆起電圧e_iと回転数Nが比例することが分かる。 よって回転数Nがあがれば逆起電圧があがり、コイルを流れる電流i(t)が下がり、トルクが下がる。

DCモータとは


　一般的に言う直流モーターであり、直流電源で回すことができる。 ＤＣモーターは制御用モーターとして非常に優れた回転特性を有している。 例えば、大きな起動トルク、電圧変化に対するリニアな回転特性、入力電流に対する出力トルクの直線性、出力効率の良さなどおよそ制御用モーターに要求されるすべての性能を兼ね備えたモーターといえる。
※トルクとは、モーターの回転力のことであり、これが大きいほどその出力パワーも大きくなる。 ここでトルクとは日本語に訳すと回転力ということになるが、このトルクは直線運動における推進力に相当する。 また、トルクの単位は［kgf・m］で表されるが、これをＳＩ単位系になおすと［N・m］になる。

DCモータの概要

　MIRSのモータパワー制御は大きく分けて2つの部分から構成される。 一つ目は、モータの回転数、方向の命令をISAバスから受けてその信号を速度信号と方向信号に変えてモータパワー制御ボードに送る部分でFPGAボード内に形成される。 もう1つは、その信号をアナログ信号に変換して実際にモータを駆動させるモータパワー制御ボードである。 そしてこの二つはドーターボードを介して接続されている。 モータの制御方法としては、PWM制御というものを採用している。




モータの電流と回転数との関係

　モータートルクＴは一般に、モーター自身のトルク定数をKtとすると、流れる電流Iaに比例する。
　　　　　T=K_t×I_a
これより、モーターに流れる電流は、
　　　　　I_a=T÷K_t
となる。又、モーターの回転数Nは、逆起電圧Ecとほぼ比例する。
　　　　　E_c(N)=E_a-R_a×I_a より、
　　　　　N=E_c(N)/(E_c÷N')
[Ec(N)：モーター仕様の逆起電圧C[V]（N'[rpm]）］
という関係がある。


最大トルク

　電源電圧がモーターに供給されている時の関係式は、 　　
　　　E_a＝R_a×I_a＋E_c 　
Eaが供給された直後はモーターが回転していないので、Ecは０である。従ってモーター起動時の式は、
　　　　　E_a=R_a×I_a
　　　　　I_a=E_a÷_a
である。Iaは、このモーターの起動時の電流であり、これがこのモーターの最大電流である。 （この時モーターは最大トルクを生じる。 最大トルクを生じるのはこの時と過負荷で動けない時であり、過負荷が最大トルクを上回っていて起動できない時、　W=I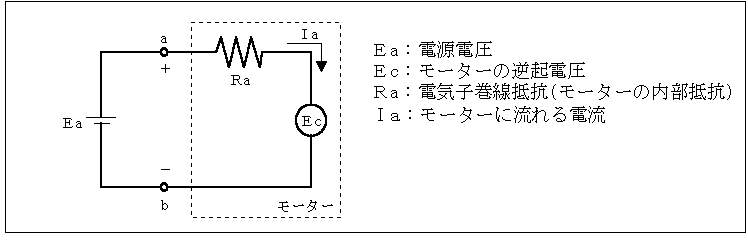a²×R_a　のジュール熱を生じ、その熱によりモーターを損傷する恐れがある。 従って、負荷は最大トルクの30〜50%位にする。）
fig.1 モータ起動時の回路



モータ特性カーブ

モーターの性能

• モーターの電気的時定数(time constant)τｅを小さくする。
  τｅ＝L/Ra　（L:等価インダクタンス、Ra:巻線抵抗）
  ※時定数とは、変化の速度を表わす指標である。 　
  　電気的時定数とは、モータを拘束しておき、電機子に定電圧を印加してから電流がその飽和値の63%まで立ち上がるのに要する時間である。 これより、巻線抵抗が大きく、等価インダクタンスが小さければ良いことが分かる。
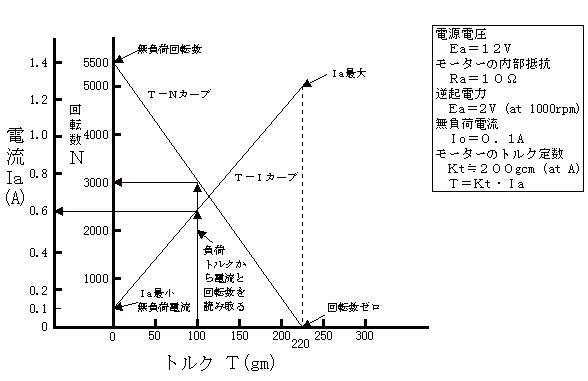
  fig.2モーターのT-N,T-I曲線
  
• 機械的時定数τｍを小さくする。
  　　　　　τｍ＝(Jm)／(Ke・Kt）　　　　(Jm：ロータイナーシャ、Ke:逆起電力定数
  　　　　　　　　　　　　　　　　　　　　Ra:電機子巻線抵抗、Kt:トルク定数）
  　従って、Jm、Raは小さく、Ke、Ktを大きくすればよい。
  ※機械的時定数...... 停止状態から無負荷回転数の63%まで加速するのに要する時間である。
  
  
• N-Tカーブのリニアリティをよくする。
  　理想的には、ＩとＮは比例、ＴとＮは逆の比例関係になるが、実際は、Nの上限で特性が曲がったり下限でリプルを生じる。従って、多スロット型、スロットレス型のモーターを選ぶ必要がある。
  　※（トルク）リプル......　出力トルクの変動分を、平均トルクに対する百分率で示すもの。この値が大きいと軸振動や騒音がひどくなる。
  スロット......　スロットとは、回転子鉄心の"溝 "である。これがあると、軸の固有振動数が変わるので、それによってモーターの振動との共振を避け、騒音を抑えられる。スロットレスモーターはスロットを持たないものをいうが、別名で平滑鉄心モーターともいう。 　

  table.1 DCモーターの特性を表す記号

  記号	名称	単位	記号	名称	単位
  Tt	全発生トルク	N・m	Ea	電機子端子電圧	V
  Ta	有効出力トルク	N・m	N	回転数	rps(rpm)
  To	損失トルク	N・m	Ra	電機子抵抗	Ω
  Nt	無損失時の無負荷回転数	rps(rpm)	Ec	逆起電圧	V
  Na	無負荷回転数	rps(rpm)	η	効率	%
  It	起動電流	A	ηm	最高効率	%
  Io	無負荷電流	A	W	出力	W
  Km	トルク定数	N・m/A	Wm	最高出力	W
  ω	回転角速度	rad/sec	Ke	逆起電力定数	V/rpm

駆動系のモーター仕様

　MIRSのモータはmaxon社製のエンコーダ、ギヤ一体型のモータを使用する。



table.2 モータデータ1

定格出力	20[W]	最大連続トルク	24.45[mNm]
公称電圧	18.00[V]	公称電圧時最大出力	55200[mW]
無負荷回転数	10200[rpm]	最大効率	83.2[%]
停動トルク	219[mNm]	トルク定数	16.3[mNm/A]
回転数／トルク勾配	48.1[rpm/mNm]	回転数定数	585[rpm/V]
無負荷電流	53.9[mA]	機会的時定数	4.63[ms]
起動電流	13400[mA]	ロータ慣性モーメント	9.19[gcm2]
端子間抵抗	1.34[Ω]	端子間インダクタンス	0.12[mH]
最大許容回転数	11000[rpm]	熱抵抗(ハウジング／周囲間）	14.00[K/W]
最大連続電流	1500[mA]	熱抵抗(ロータ／ハウジング間）	3.10[K/W]

• MIRS技術調査報告書